Projenin Kodları
Tüm projeyi İNDİR: Program Kodu ve Rapor
1.Giriş
Bu çalışmada bir kroki üzerinde bulunan noktalar arası rota ve yolun genetik algortima ile bulunması amaçlanmıştır. Genetik algoritma rastgele arama metodu olduğu için tek bir çözüm aramak yerine bir çözüm kümesi üzerinde çalışır. Optimum çözüme olası çözümlerin bir bölümü üzerinde gidilir. Böylece çalışmadaki sonuçlar her zaman en iyi olmaz. Çalışmada genetik algoritmanın kullanılmasının nedeni, genetik algoritmanın problemin doğasıyla ilgili herhangi bir bilgiye ihtiyaç duymamasıdır. Temelinde gezgin satıcı problemine benzeyen çalışmanın , gezgin satıcı problemine benzer problemler içinde çözüm olması amaçlanmıştır.
2.Genetik Algoritma Yönteminin Probleme Uygulanışı
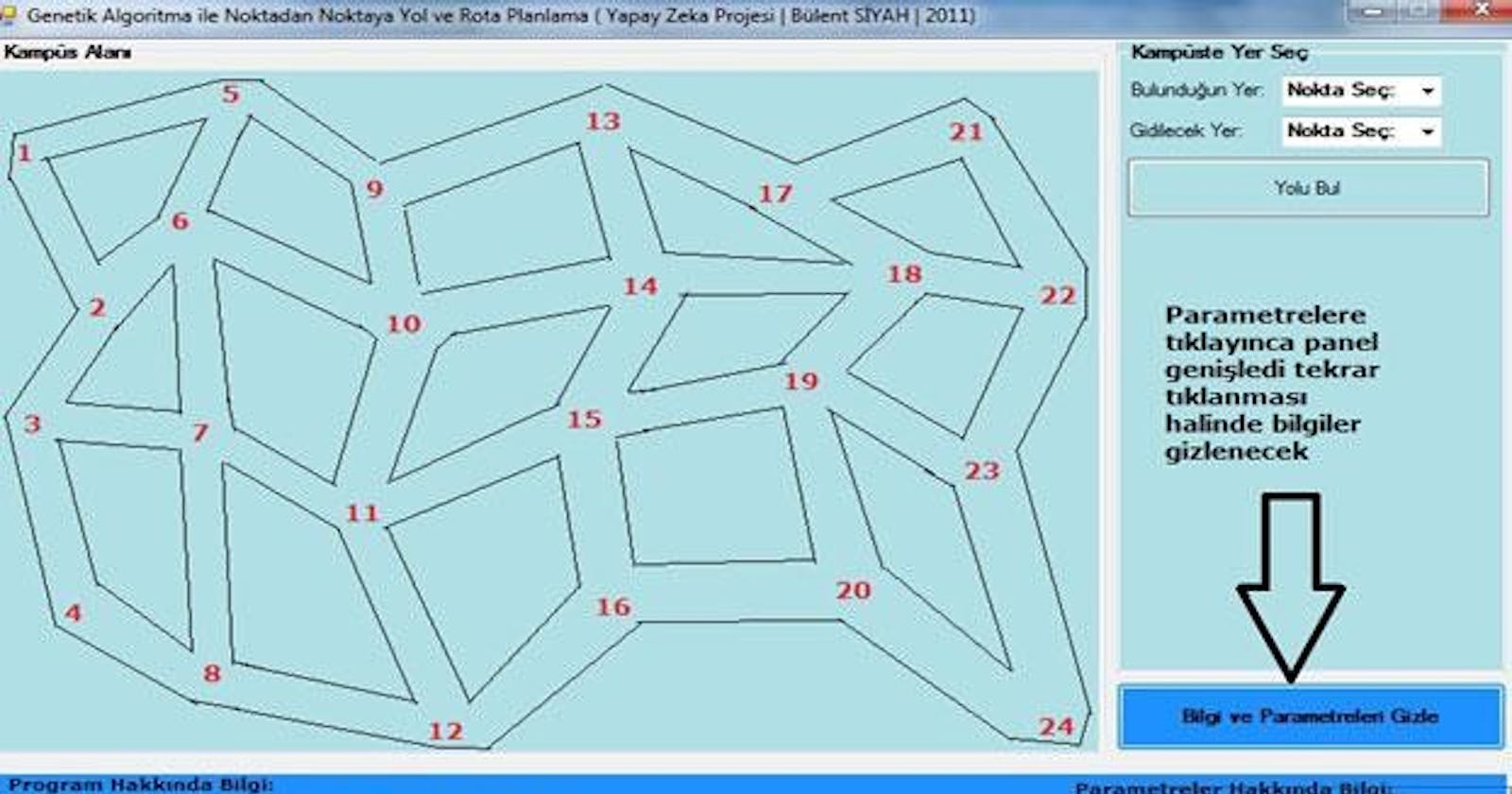
Problemin çözümü için populasyon büyüklüğü karar verilmelidir. Populasyon büyüklüğü seçilirken aşırı yüksek seçilirse gelişim yavaşlar, aşırı küçük seçilmesi durumunda da araştırma uzayı yetersiz olur. Problemimize en uygun populasyon büyüklüğü 30 birey olarak seçilmiştir. Programın arayüzünde birey sayısı değiştirilebilir. Her kromozom 20 genle temsil edilip, genler kodlanırken değer kodlama yöntemi kullanılmıştır. Her gen yönleri temsil eden 0;Batı, 1;Kuzey, 2;Doğu ve 3;Güney ile belirtilmiştir. Örnek olarak 5 nolu kromozomun genleri:01102033021011023221 gibi 20 gene sahiptir.
Populasyon büyüklüğü tamamlanıp, kromozomlar kodlandıktan sonra uygunluklarına göre seçilim yapıldı. Uygunluk değerleri hesaplanırken noktalar arası seyahat olduğu için kromozomun en son noktası ile ulaşmak istenen arasındaki farka bakılır. Bu yüzden uygunluk fonksiyonumuz 2 fonksiyonun toplamına eşittir. Birinci fonksiyonumuz en son nokta uzaklığı f(y) , ikinci fonksiyonumuz ise kromozomun aldığı yolların toplamı olan toplam mesafe f(z) fonksiyonudur. Uygunluk fonksiyonumuz f(x)=5*f(y)+ f(z) olarak belirlenmiştir. Burada son nokta uzaklığını fonksiyonu problem için daha önemli olduğundan katsayısı artılmıştır. Örneğin 6 nolu kromozom son noktası 21 , ulaşılmak istenen nokta 22 ise f(y)=20, ve aldığı yolların mesafesini ölçen f(z)=550 olduğunu düşünelim ,6 nolu kromozomun uygunluk değeri f(x)=5*20+550=650 olur. Kromozom ulaşılmak istenilen noktaya varmış olsaydı bu değer 550 olacaktı. Burada görüldüğü gibi son noktaya ulaşmak uygunluk değerini hesabının doğruluğunu kanıtlıyor.
Seçilimde ikili turnuva seleksiyonu kullanıldı. İkili turnuva seçiminde populasyon içinden rastgele iki birey seçilir ve uygunlarına göre iyi olan alınır, daha sonra tekrar rastgele iki birey seçilir ve yine uygunluklarına göre en iyi olan alınır. Böylece elde olan iki tane birey çaprazlanarak yeni topluma katılır. Çaprazlama yapılırken rastgele bir lopus seçilir ve iki kromozom o lopustan değiştirilir. Örnek rastgele 2 ve 16 nolu bireyler seçildi bunlardan uygunluğu en iyi olan 2, tekrar rastgele iki birey seçildi 11 ve 7, bunlara arasındada uygun olan 7 , bu kazanan 2 ve 7 bireyi rastgele bir noktadan değişirme hazırlar. Rastgele noktamızın 9 olduğunu düşünürsek her kromozom 20 gen olduğu için ilk 9 gen 2 nolu kromozomdan geriye kalan 11 gen 7 nolu kromozomdan alınır(2 ile 7 ikili turnuva sonucunda eşleşen kromozomlardı). Aynı işlem 7nin ilk 9 geni alınır geriye kalan 11 gende 2den alınır. Turnuva metodun da seçilen birey tekrar sisteme dahil edilir yani çaprazlamaya uğrayan birey tekrar çaprazlamaya katılabilir.
Populasyondaki en iyi birkaç birey doğrudan yeni topluma aktarıldı. Geriye kalan bireyler çaprazlama ile yaratıldı. Çaprazlamaya ugrayan bireylerden biri mutasyona uğratıldı. Mutasyon yapılmasının nedeni önceki çözümlerin kopyalanmasını önlemek. Mutasyon için rastgele bir gen seçilir ve değiştirilir. Böylece yeni populasyon oluşturuldu. Problemin çözümü için belirelenen iterasyon sayısı kadar döngü devam eder. Döngü sonlanınca problemin en ugun çözümü elde edilmiş olur. Böylece optimum değer elde edilmiş oldu fakat çalışmanın diğer amacı olan alternatif yollar üretmek için son nesilden önceki nesillerin tümünden en iyi olanlarda seçilip , seçilen yollar arasından birbirinden farklı olan diger yollarda projede tutularak arayüzde yansıtıldı.
3. Performans Analizi
Problemin çözümünde elde edilen bazı veriler;
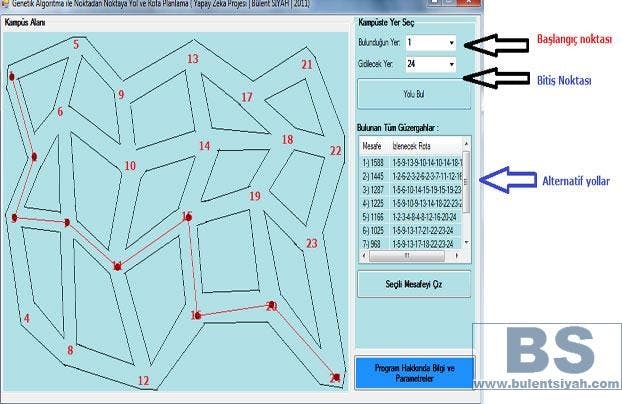
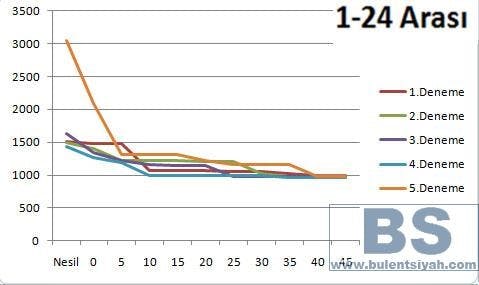
Başlangıç noktasından bitiş noktasına gitmeye çalışınca elde edilen veriler grafikte gösterilmiştir. Y ekseni Uzaklık piksel , x ekseni nesil sayısnı gösterir.
4.Sonuçlar ve Öneriler
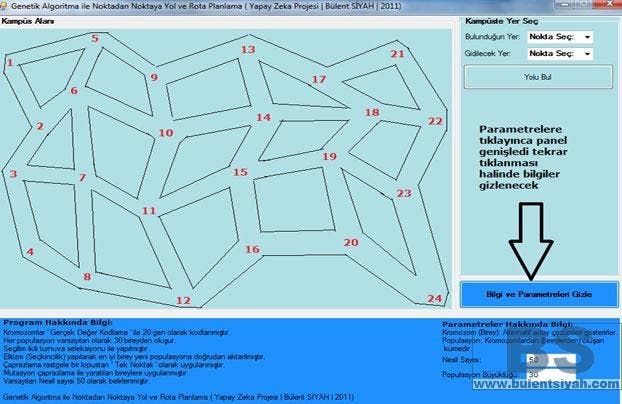
Elde edilen tüm sonuçlara göre bir probleme genetik algoritma uygulanmasında uygun parametreler seçilmediği taktirde en uygun çözümden uzaklaşır. Çalışmada populasyon büyüklüğü ayarlanırken varsayılan değer olan 30 ile 100 değeri arasında gözlemlerim; populasyon büyüdükçe çözüm olması muhtemel bireylerin çoğalması ve çözüm uzayının genişlemesiyle en iyiye daha da yaklaşılmıştır.
Uygunluk fonksiyonu oluşturulurken çalışma için önemli noktalar belirlenmemesi halinde uygun olmayan bireyler uygun sanılıp problemin çözümünden uzaklaşılır. Bu çalışmada uygunluk fonksiyonu 2 tane fonksiyonun toplamına eşit. Çünkü en kısa yol bulunmasının dışında önemli olan parametre kromozomun istenilen noktaya ulaşıp ulaşmadığıdır. Yönetimin probleme uygulanışında bir örnek ile bu durumun anlatılmaya çalışıldı.
Seçilim için ikili turnuva seçilimi haricinde rulet tekeli seçilimi çalışmada kullanılmamasının sebebi rulet tekeri yöntemi ile iyi olan birey nesiller sonra kendisiyle aynı bireyler üreterek çözüm uzayını o nokta etrafında toplamasıdır. Bu durum çalışmada daha iyi olması muhtemel çözümlerin araştırılmasını engellediğinden kullanılmamıştır.
Çaprazlamada ise çaprazlama oranının probleme uygun ayarlanmaması halinde çalışmada hatalar gözlendi. Örneğin en iyi bireylerin yok olması istenilen bir durum değildi ve tüm bireyler çaprazlama ile oluşturulması durumunda bu hata açığa çıktı. Bu durumu engellemek için elitizm yapılarak en iyi bireyler doğrudan yeni topluma aktarılarak elenmeleri engellenmiş oldu. Çaprazlama sayesinde çözüm uzayı genişledi. En iyi bireyler doğrudan yeni topluma aktarılmasına rağmen ikili turnuva yönteminde kullanılan kümeden çıkarılmadılar. Çaprazla için seçilen bireyler de ikili turnava yöntemi için bulunan kümesinden çıkarılmadı.
Mutasyonun çözüm yoğunluğunu dağıttı gözlendi. Fakat mutasyon oranı fazla tutulması halinde en uygun değerden uzaklaşıldığı izlendi. Bu yüzden çalışmamızda mutasyon oranı 0.01 olarak tutulmasına karar verildi.
Projenin geliştirlmesi halinde bir bina içerisinde özellikle çok sayıda geçiş bulunduğu karmaşık binalarda istenilen yerler arasında en uygun şekilde yol ve rota bulunabilir. Çalışmanın ileriki aşamalarında program arayüzüne kullanıcı tarafından kroki,harita veya plan yüklenmesi sağlanabilir. Gezgin satıcı problemine benzer problemler için de kullanılabilir. Örneğin bilgisayar ağlarında olası bir kopmada diğer en uygun yollar bulunabilir.