Projenin Kodları
Tüm projeyi İNDİR: Program Rapor ve Kodu
1. GİRİŞ
Bu çalışmada, çift taraflı mondaj hattının her iki tarafı için belirlenmiş çevrim süresi içerisinde istasyon sayısını en aza indirgeme amaçlanmıştır. Operasyonlarda taraf ve istasyon sayısı kısıtları bulunmaktadır. Problemin Genetik Algortima ile çözümü için geliştirilen uygulama, c#(sharp) programlama dili ile yazılmıştır.
Genetik algoritma rastgele arama metodu olduğu için tek bir çözüm aramak yerine bir çözüm kümesi üzerinde çalışır. Optimum çözüme olası çözümlerin bir bölümü üzerinde gidilir. Böylece çalışmadaki sonuçlar her zaman en iyi olmaz. Çalışmada genetik algoritmanın kullanılmasının nedeni, genetik algoritmanın problemin doğasıyla ilgili herhangi bir bilgiye ihtiyaç duymamasıdır.
2. Materyal ve Yöntem
Genetik Algoritmalar, daha iyi çözümlere yavaş yavaş bir yaklaşım sağlayan geniş bir problem uzayı boyunca yönlendirilmiş rastgele bir araştırmaya imkan sağlar. Temel avantajı optimize edilmeye çalışılan problemin doğasıyla ilgili herhangi bir bilgiye ihtiyaç göstermemeleridir.
2.1. GENETİK ALGORİTMALARIN TEMEL KAVRAMLARI
Evrimsel hesaplama topluluğunda yerleşik, tek bir Genetik Algoritma tanımı bulunmamakla beraber, Genetik Algoritma sınıfına girdiği kabul edilen yöntemlerde en azından şu ortak unsurlara rastlanır: kromozom topluluğu, uygunluğa göre seçilim, yeni bireyler üretmek için çaprazlama, yeni bireylerin rastgele mutasyonu. Holland'ın GA'nın unsurları içinde saydığı ters çevirme operatörü günümüzde nadiren kullanılmaktadır.
2.1.1. Kromozom ve Topluluk
GA'da kromozomlar, problem için olası çözümleri temsil ederler. Bu çözümlerden her birine birey adı verilir. Topluluk (popülasyon) kromozomlardan (bireylerden) oluşan kümedir. GA'nın kromozom toplulukları üzerinde işlemler yapması ile, bir önceki topluluklar her seferinde yeni üretilen topluluklarla yer değiştirir.
2.1.2. Uygunluk
Uygunluk değeri, çözümün kalitesini belirler ve uygunluk fonksiyonu kullanılarak hesaplanır. Uygunluk fonksiyonu mevcut topluluktaki her kromozoma bir puan (uygunluk değeri) atar. Kromozomun uygunluğu, o kromozomun eldeki problemi ne kadar iyi çözdüğüyle ilişkilidir.
2.1.3. Genetik Operatörler
GA'nın en basit formu üç tip genetik operatör içerir: seçilim, çaprazlama (çift noktalı) ve mutasyon.
Seçilim: Bu operatör topluluktaki kromozomları üreme için seçer. Kromozomun yüksek uygunluk değerine sahip olması, üremek için seçilmesi ihtimalini arttırır.
Çaprazlama: Bu operatör rastgele iki lopus belirleyip, iki kromozomun bu lopuslardan önceki ve sonraki kısımlarını aynı kalıcak şeklide, lopus aralarındaki kısımları değiştirilerek gerçekleştirilir.
Mutasyon: Bu operatör kromozomdaki bir veya daha fazla rastgele alınan bireyin yine rastgele seçilen gen ile genin değerine sahip diğer genin değişimi ile olur.
2.2. GENETİK ALGORİTMA PARAMETRELERİ
2.2.1. Topluluk Büyüklüğü
Topluluk büyüklüğü için seçilen değer, algoritmanın performansını iki şekilde etkilemektedir. Birincisi, topluluk büyüklüğünün aşırı küçülmesi araştırma uzayının yetersiz örneklenmesine sebep olacağından
kontrollü ıraksamayı sağlamak zorlaşacak ve araştırma belirli bir alt optimal noktaya doğru sürüklenecektir. ikincisi, topluluk için aşırı yüksek değer seçildiğinde bir nesillik gelişim oldukça uzun süreye ihtiyaç duymaktadır.
2.2.2. Çaprazlama Oranı
Bireylerin çoğalması sırasında kromozomlara uygulanacak çaprazlama operatörünün frekansını belirlemek amacıyla kullanılan parametredir. Düşük çaprazlama oranı yeni nesle çok az sayıda yeni yapının (ebeveyninden farklı yeni bireyler) girmesine sebep olmaktadır. Dolayısıyla tekrar üreme operatörü algoritmada aşırı etkili bir operatör haline gelmekte ve araştırmanın yakınsama hızı düşmektedir. Yüksek çaprazlama oranı araştırma uzayının çok hızlı bir şekilde araştırılmasına sebep olmaktadır. Ama oran aşırı yüksek ise, çaprazlama operatörü
benzer veya daha iyi yapıları üretmeden kuvvetli olan yapılar çok hızlı olarak bozulduğundan, algoritmanın performansı düşmektedir.
2.2.3. Mutasyon Oranı
Mutasyon operasyonun frekansı, etkili bir genetik algoritma tasarlamak için çok iyi kontrol edilmelidir. Mutasyon operasyonu, araştırma sahasına yeni bölgelerin girmesini sağlar. Yüksek mutasyon oranı, araştırmaya aşırı bir rastgelelik kazandıracak ve araştırmayı çok hızlı olarak ıraksatacaktır. Başka bir deyişle, topluluğun gelişmesine değil tahribatına sebep olacaktır. Bu durumun tersine, çok düşük mutasyon oranının kullanılması ıraksamayı aşırı düşürecek ve araştırma uzayının tamamen araştırılmasını engelleyecektir. Dolayısıyla, algoritmanın alt optimal çözüm bulmasına sebep olacaktır.
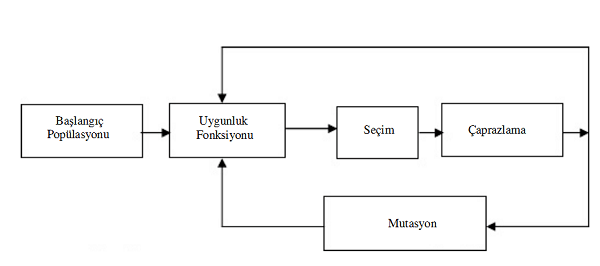
2.3. GENETİK ALGORİTMA SÜRECİ
Çözülmek üzere tanımlı bir problem verilmesi ve aday çözümlerin birer sayı dizisi ile temsil edilmesi halinde, GA şu şekilde çalışır:
1. N adet kromozom (problem için aday çözümler) içeren rastgele oluşturulmuş bir topluluk ile başla.
2. Topluluktaki her x kromozomu için f(x) uygunluk değerini hesapla.
3. Aşağıdaki adımları birey n (topluluk büyüklüğü) oluşturuluncaya kadar tekrarla.
3.a. Güncel topluluktan, yüksek uygunluk değerinin seçilme ihtimalini arttırdığını göz önünde bulundurarak, iki ebeveyn kromozom seç. Seçilim, aynı kromozomun birden çok defa ebeveyn olarak seçilmesine olanak verecek şekilde yapılır.
3.b. Pc olasılığı ("çaprazlama olasılığı" ya da "çaprazlama oranı") ile seçilen çifti iki yeni birey oluşturmak üzere rastgele belirlenen iki noktadan çaprazla. Eğer çaprazlama gerçekleşmezse ebeveynlerinin birebir kopyası olan iki çocuk oluştur. Pc için iki noktalı çaprazlama yöntemi seçilmiştir.
3.c. Pm olasılığı ("mutasyon olasılığı" ya da "mutasyon oranı") ile, oluşan bir veya birden fazla çocuğu tüm veya bazı lopuslarında mutasyona uğrat. Lopuslardaki genlerin değiştirilmesi ile de mutasyon gerçekleştirilir.
3.d. Sonuçta elde edilen kromozomları yeni topluluğa ekle.
4. Önceki topluluğu yeni topluluk ile değiştir. Böylece yeni nesil elde edilmiş oldu.
5. Sonlandırma koşulu sağlandıysa mevcut topluluktaki en iyi çözümü döndür, sağlanmadıysa 2. adıma dön. Sonlandırma koşulu çoğu zaman nesil sayısıdır. Bazı genetik algortimalarda bu koşul, belirlenen aralıkta uygunluk değerine sahip birey elde edilmesi olabilir.
2.4. SÜRECİN PROBLEME UYGULANIŞI
2.4.1. İlk Toplum Oluşturulması ve Kromozomların Kodlanması
Bir GA programının yazılması işleminde karşılaşılan ilk problemlerden biri kromozomların kodlanmasıdır. Kodlama işlemi problemin türüne göre değişmektedir. Bazen binary (ikili) kodlama en iyi çözüm bulmada kullanılırken, bazen de permutasyon veya değer kodlama yöntemleri optimum sonucu bulmada en uygun kodlama yöntemi olabilir. Permutasyon kodlama yöntemi, genel olarak gezgin satıcı ve şebeke tasarımları gibi sıra gözeten problemlerde yaygınca kullanılır.
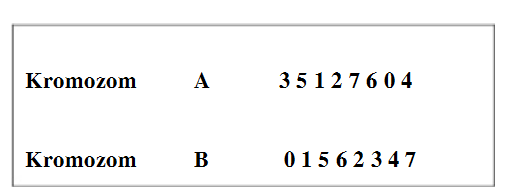
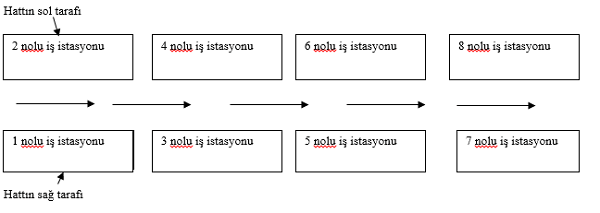
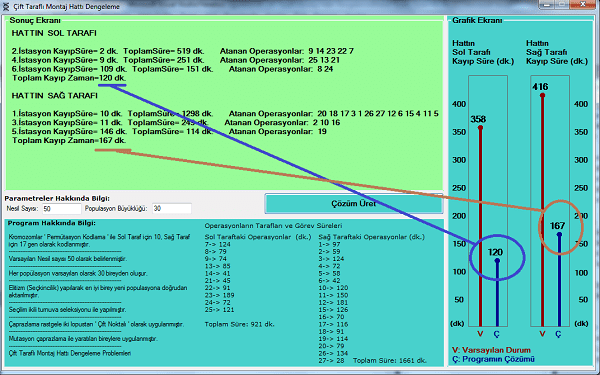
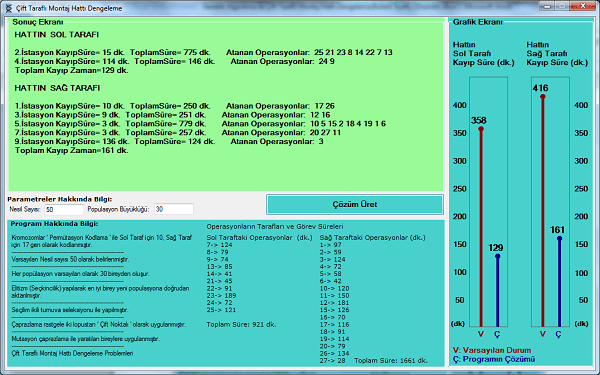
Problemin çözümü için populasyon büyüklüğü karar verilmeli, populasyon büyüklüğü seçilirken aşırı yüksek seçilirse gelişim yavaşlar, aşırı küçük seçilmesi durumunda da araştırma uzayı yetersiz olucağından problemimize en uygun populasyon büyüklüğü 30 birey olarak seçilmiştir. Programın arayüzünde birey sayısı değiştirilebilir. Problemde permutasyon kodlama yöntemi seçilip, hatların taraflarındaki operasyon sayıları farklı olduğundan, hattın sol tarafı 10 operasyon dolayısıyla 10 gen ile, hattın sağ tarafı 17 operasyon yani 17 gen ile temsil edilmiştir. Her gendeki sayı değeri operasyon numarasına eşittir. Örnek olarak hattın sol tarafındaki 7 nolu kromozomun genleri: 4051296741038 şeklinde kodlanmıştır.
İlk toplum oluşturulurken tüm bireylerin genleri rastgele oluşturulmuştur. Problemde ilk toplumu oluşturan fonksiyon sadece ilk nesilde çalışır. Diğer nesillerde zaten eski ve yeni nesil değişimi gerçekleştiğinden bu fonksiyon kullanılmaz. Fonksiyon, birey sayısı kadar dönen döngüde her birey için gerekli gen sayısı kadar rastgele sayı üretir. Permutasyon kodlama ile yapılırken aynı gen değerine sahip bireylerin oluşması engellenmiştir.
2.4.2. Toplumdaki Her Kromozomun Uygunluk Değerinin Ölçülmesi
Popülasyon içerisinde yer alan ve her bir bireyi temsil eden kromozomların ne kadar iyi olduklarını bulan fonksiyona uygunluk fonksiyonu (uyumluluk, fitness) fonksiyonu denir. Bu GA programında özel çalışan tek kısımdır. Uygunluk fonksiyonu kromozomların şifrelerini çözer (decoding) ve sonra da hesaplama yaparak bu kromozomların uygunluklarını hesaplar.Elde edilen uygunluk değerlerine göre kromozomların yeni generasyon da olup olmayacaklarına karar verilir. Bütün popülasyonun (topluluğun) uygunluk değerleribelirlendiğinde sonuçlandırma kriterinin sağlanıp sağlanmadığına bakılır. Sonuçlandırma kriteri birkaç şekilde seçilebilmektedir. Bu seçeneklerden biri, istenilen nesil sayısına ulaşılması olabileceği gibi, tüm topluluğun uygunluk değerinin en iyi çözümün uyumluluk değerine oranının yeterli görülen bir değere ulaşması olabilir.
Uygunluk değerleri şöyle hesaplanır. Genler operasyonları temsil edip, sıra ile gruplandırılarak işçinin net çalışma süresi(260 dk.) ile işlemlerden geçirilip, kayıp zaman bulunarak hesaplanır. Buradaki gruplam için şart belli bir eşik değere göre yapılır. Eşik değeri sağlayan operasyonlar yani genler aynı grupta yer alarak o istasyona atanır. İşçinin çalışma süresi ile işlemler şunlardır. Eşik değeri sağlayan gen grubunun tüm süreleri toplanır. Bu toplam değer işçinin çalışma süresine göre modu alınır. Alınan mod ile elde edilen değer kalan değeridir. Toplam değer yine işçinin çalışma süresine göre normal bölme işleminden geçirilir. İşlem sonucunda elde edilen değer bölüm değerdir. Uygunluk değeri için ilk olarak işçinin çalışma süresi ile elde edilen kalan değer çıkartılır. Bu değer, elde edilen bölüm süresinin bir fazlası ile çarpılarak uygunluk değeri hesaplanır. İşlemlerde şu ayrıntı önemlidir. Eşik değeri geçememe ihtimali olursa tüm operasyonlar tek istasyonda toplanır. Bu istenmeyen durum için kayıp zaman, tüm operasyonların toplamı ile elde edilir. Böylece problemde bu adımda tekli gruplamanın uygunluk değeri yüksek olduğundan elenme ihtimali çok yükselir. Uygunluk fonksiyonunda eşik değer istenilirse her iki hattın tarafı için ayrı değerlere sahip olabilir. Fonksiyon sonrasında tüm bireylerin uygunluk değerleri bir dizide toplanır. Dizilerin birbirleriyle indexleri sayesinde anlaşırlar.
2.4.3. YENİ TOPLUM OLUŞTUR
2.4.3.1. Elitizm Yapılması
Elitizm, performansı en iyi bireyle (bireyler) temsil edilen o ana kadar ki en iyi çözümün korunarak, değiştirilmeksizin bir sonraki nesle aktarılmasını sağlar. Toplumda tüm bireyler çaprazlanarak oluşturulursa, iyi olan bireylerin yok olma veya çözümden uzaklaşma ihtimali ortaya çıkar. Bu durumu ortadan kaldırmak için toplum içindeki en iyi 2 tane birey direk yeni topluma eklenerek elitizm yapıldı. Elitizm yapıldığı fonksiyonda en iyi uygunluk değerine sahip bireylerin seçilmesi dışında tüm bireyler uygunluk değerlerine göre sıralandı. Böylece çarpazlama için seçilen bireylerin kıyaslama işlemleri daha kolay gerçekleştirildi.
2.4.3.2. Seçilim ve Çaprazlama
En iyi kromozomları seçmek için birçok yöntem vardır. Bu seçim yöntemlerinden bazıları; Rulet tekerleği seçimi (roulette wheel selection), Boltzman seçimi (Boltzman selection), turnuva seçimi (tournament selection), sıralama seçimi (rank selection) ve sabit durum seçimidir. Seçilimde ikili turnuva seleksiyonu kullanıldı. İkili turnuva seçiminde populasyon içinden rastgele iki birey seçilir ve uygunluklarına göre iyi olan alınır, daha sonra tekrar rastgele iki birey seçilir ve yine uygunluklarına göre en iyi olan alınır. Böylece finale kalan iki tane birey çaprazlama işlemi için seçilmiş olur.
Genel olarak çaprazlama işlemi; kromozomların nasıl kodlanacağı belirlendikten sonra popülasyondaki kromozomlardan uygunluk değeri yüksek olanlar içerisinden rasgele seçilen iki birey arasında, yine rasgele seçilen bir noktaya göre karşılıklı gen alış-verişi olarak tanımlanır. Çaprazlama işlemi, uygunluk değeri iyi olan ve rasgele seçilen iki kromozomdan daha iyi uygunluk değerine sahip, yeni kromozomların elde edilmesi amacıyla yapılmaktadır. Yeni neslin uygunluk değerlerinin iyi çıkması ve problemin optimum çözüme ulaşabilmesi açısından çaprazlama işlemi son derece önem taşımaktadır. Bu aşamada, faklı kromozomlar alınarak çaprazlama işlemi yapıldığı için değişik özelliklerin test edilmesine ve hızlı olarak yeniden oluşmasına olanak sağlar. Bu işlem neticesinde ise, iki bireyin kopyası durumundaki kopyalanmış bireyler ile çeşitlilik sağlanmış ve en iyi çözüme yaklaşım sağlanmıştır. Çaprazlama için uygulamada iki noktalı çaprazlama seçilmiştir. Bu tür çaprazlama işleminde iki tane kırılma noktası alınır. İlk noktaya kadar olan bitler birinci kromozomdan, iki nokta arasındaki bitler ikinci kromozomdan, kalanlar ise tekrar birinci kromozomdan yeni bireye kopyalanırlar.
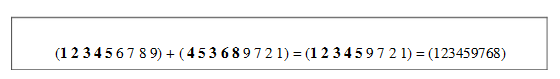Uygulamada seçilen ikili turnuva metodunu uygulamak için toplumda rastgele 2 şer birey alınıp birbirleriyle kıyaslanır. Bu kıyaslama işlemini, daha önce elitizm fonksiyonunda yapılmış olan bireylerin uygunluklarına göre sıralanmış olması kolaylaştırır. Çünkü rastgele elde edilen sayıların, sayı değerlerini kıyaslamak yeterli olacaktır. Çaprazlama için seçilen iki bireyler iki noktalı yöntem ile çaprazlanıp yeni topluma aktarılır.
2.4.3.3. Mutasyon
GA programının sonuca ulaşmasında önemli olan başka bir etkende mutasyon işlemidir. Programın belirli bir alana yoğunlaşarak sonuca ulaşmayı engelleyen bazı durumlarda, problemin daha geniş bir alanda arama yapabilmesi için mutasyon işlemine baş vurulur. Böylelikle popülasyondaki çözümlerin yerel optimuma düşmesi engellenmiş olur. Uygulamada çaprazlamaya uğrayan bireylerden biri mutasyona uğratıldı. Mutasyon için rastgele bir birey seçilir ve yine rastgele seçilen gen ile genin değerine sahip olan diğer gen yerdeğiştirilerek gerçekleştirilir.
2.4.4. ÖNCEKİ TOPLUM İLE YENİ TOPLUMU DEĞİŞTİR
Önceki topluluğu yeni topluluk ile değiştirilir. Böylece yeni nesil elde edilmiş olur.
2.4.5. SONLANDIRMA KOŞULU KONTROLU
Problemin çözümü için sonlandırma koşulu belirelenen iterasyon sayısı kabul edilir. Döngü sonlanınca problemin en uygun çözümü elde edilmiş olur.
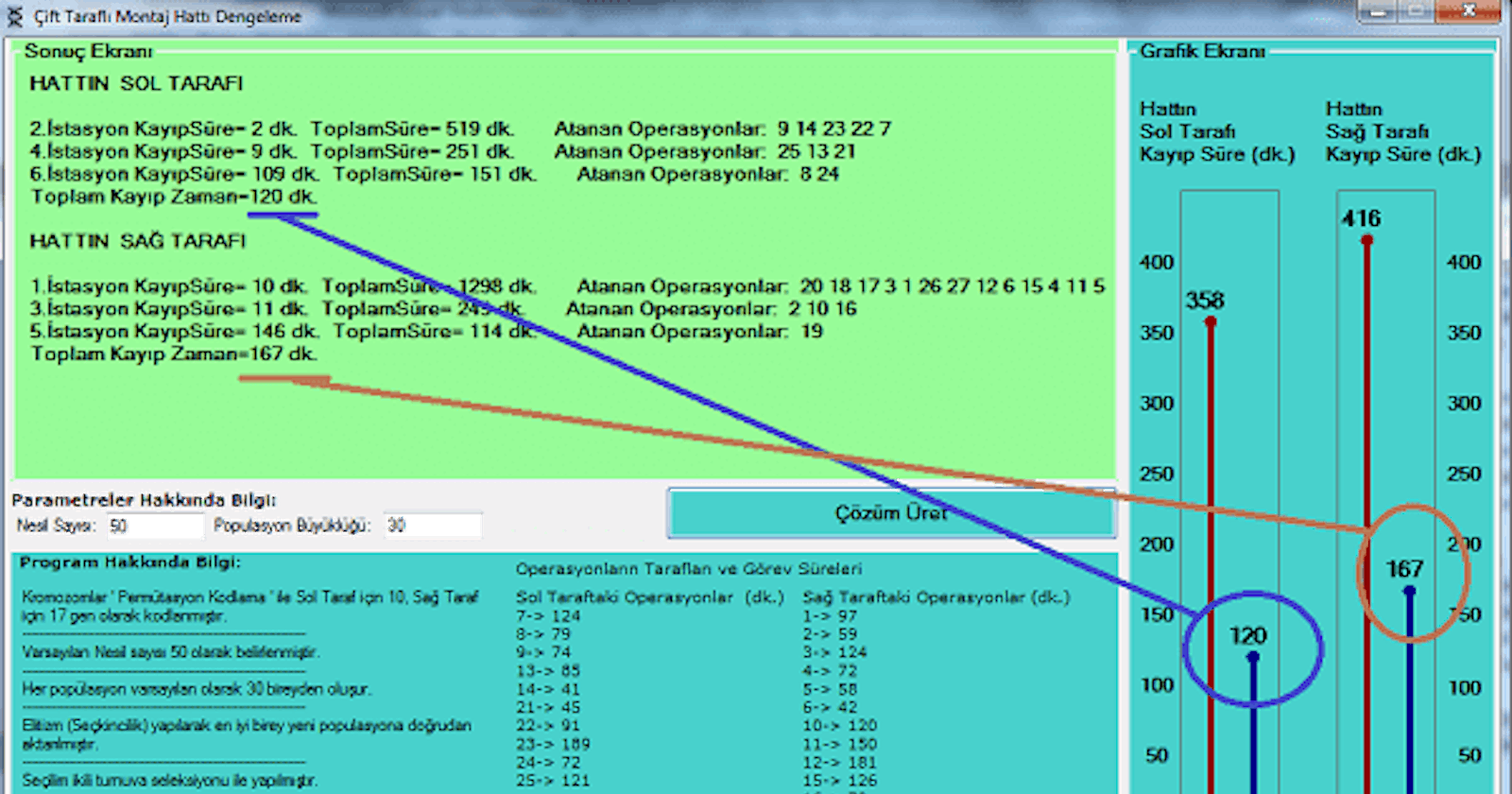
Çalışmada, çift taraflı mondaj hattının her iki tarafı için belirlenmiş çevrim süresi içerisinde istasyon sayısını en aza indirgeme hedeflenmiştir. Problemde her hattın belirli bir operasyon süresi vardır. Bu operasyonların bir araya geldiği istasyonlarda işlemleri gerçekleştirmek için operasyonların toplamı kadar süre harcanır. Bu süre bir işçinin çalışma süresinin tam katları şeklinde yerleştirilmelidir. Aksi durumda operasyonarın bitiminde işçinin bekleme yani kayıp süre oluşur. Bu uygulamada da amaç genetik algoritma ile bu süreyi olabildiğince en aza indirmek hedeflenmiştir.
3.1. OPERASYONLAR VE ÇEVRİM SÜRELERİ
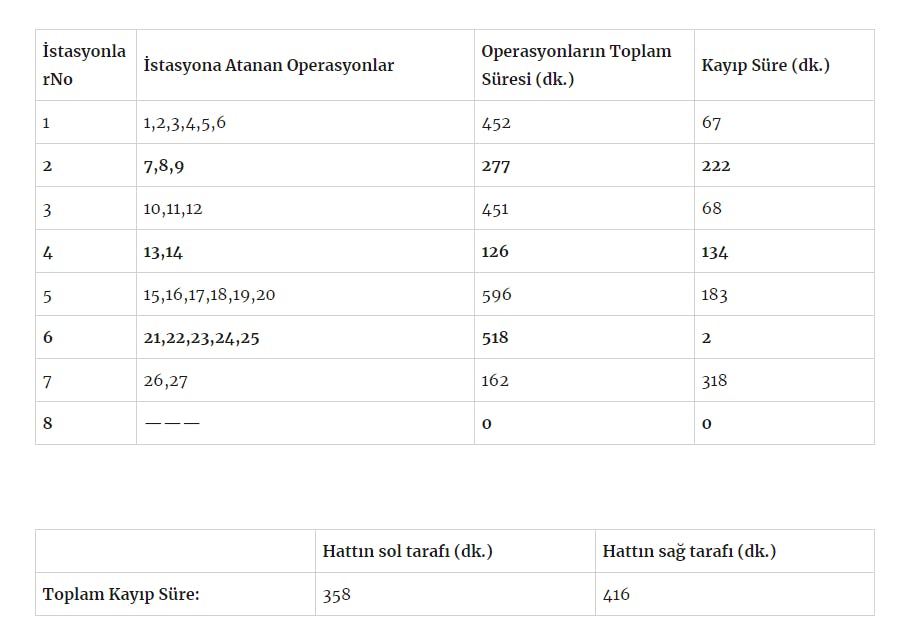
Problemin tanımlanması için her istasyon için değişmez ve ayrı olan operasyon numaraları ile bu operasyonlara ait süreler tablo şeklinde verilmiştir.
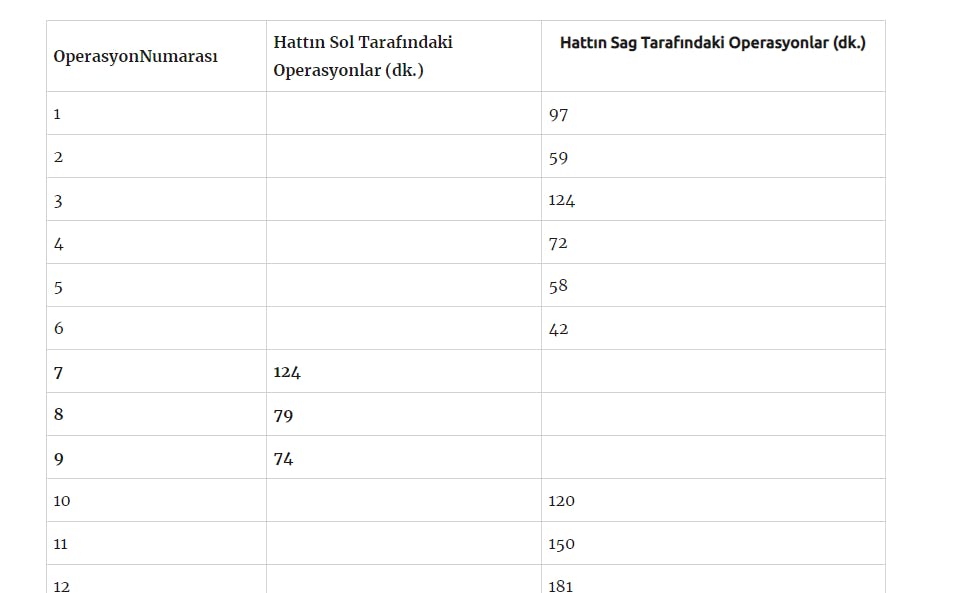
3.2. PROBLEMİN VAROLAN DURUMU
İstasyonlar için şuan ki durum :
